문제 : boj28276

필요 알고리즘
- 이분 탐색(binary search), 매개 변수 탐색(parametric search)
- 이분 탐색을 응용한 매개 변수 탐색 알고리즘 문제이다. 흔히 결정 문제라고 부르는 형태의 문제이다. 물론 결정 문제로 어떻게 만들지는 아이디어가 떠올라야 하긴 하다.
- 분리 집합(disjoint set)
- 결정 문제로 풀고자 할 경우, 분리 집합을 써야 효율적으로 짤 수 있다. 애초에 시간 제한이 빠듯한 문제라 다른 방법으론 통과가 힘들 것 같다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
우선 이 문제의 완벽한 하위호환 문제가 있다. '백준 2343 기타 레슨' 문제가 정확히 이번 문제에서 R=1인 경우에 해당하고, 기본적인 아이디어가 동일하므로 우선 백준 2343을 먼저 풀어보자. 저걸 못풀면 이 문제는 풀 수 없다 (혹은 다른 방법을 찾거나). 근데 기본적인 아이디어가 비슷한데도 이 문제는 플래고 저 문제는 실버인 이유는 직접 구현해보면 알 수 있다.. ㅠ
이번 문제는 풀이가 사람마다 상당히 달라서 재밌었던 것 같다. 풀고나서 두 분의 코드를 봤는데 나까지 포함해서 셋 다 기본 아이디어는 동일하지만 구현 로직이 달랐다 ㅋㅋ.
기본 아이디어는 이 문제를 결정 문제로 보는거다. 결정 문제가 무슨말이냐면, 만약 isPossible(int limit) 이라는 함수가 있고 이게 '추가로 하품을 하는 학생의 수의 최댓값'이 limit 이하의 수치로 W개의 칸막이를 놓을 수 있는지 판단하는 함수라고 해보자.
만약 isPossible() 함수가 유효한 시간내에 동작이 가능하다고 가정하면, limit 값은 0부터 100만(R*C 배열에 전부 1이 입력으로 들어온 경우의 최대값) 까지가 될 것이다. 그리고 limit값을 이분 탐색으로 가능한 경우를 좁혀나가면 O(log(R*C) * isPossible()의 시간복잡도)로 동작 가능하게 된다.
그럼 이제 isPossible()이 유효한 시간 내에 동작 가능하도록 짜면 된다. RxC 배열에서 i가 [0, R), j가 [0, C)를 의미한다고 해보자. 즉, arr[i][j] 형태이다.
우선 내 경우에 처음 시도했던건 단순히 bfs로 j를 1씩 증가시키면서 열 단위로 살펴보는 것이었다. j를 1씩 증가시키면서 bfs로 연결 여부를 판단하면서 보다가 연결된 부분이 limit을 넘어가면 거기에 칸막이를 (W-=1) 세우는 방식이다.
이 경우 문제는 다음과 같은 경우이다. j가 최대치일 때, bfs로 저걸 판단하려면 사실상 전체맵을 순회해야 하므로 시간복잡도가 저 멀리 가게된다.

다음으로는 Deque를 써서 각 라인마다 j의 시작 지점과 끝 지점을 둬서 어떻게 구현해보려 했으나 구현이 어렵기도 하고, 위와 같은 상황에서 마땅한 방법을 찾을 수 없어서 제외했다.
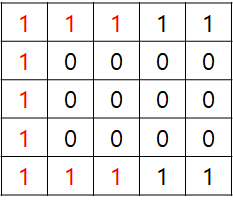
그럼 어떻게 해야 할까? 현재 만족해야 하는 부분은, 위 그림처럼 j=0인 구간을 통해 j=4인 구간의 i=0인 부분과 i=4인 부분이 서로 동일한 구간임을 쉽게 판단할 수 있어야 한다는 점이다. 여기에 딱 맞는게 분리 집합 알고리즘이다. 그래서 분리 집합 알고리즘으로 생각을 해보기 시작했다.
다만 이 경우 W=0일 때는 매우 편하게 사용할 수 있다. j = 0부터 시작해 j를 증가시키면서 동일한 분리 집합에 대해 자식이 몇 개 인지 기록하는 방식으로 처리하면(코드에선 음수가 해당 집합의 크기에 해당한다. -5면 연결된게 5개라는 의미) O(1)로 문제에서 원하는 추가로 하품하는 인원을 알 수 있다. 예를들어 아래처럼 j=0과 j=1은 이미 봤고 현재 j=2이고, i=0이라고 해보자. 분리집합에 정의된 음수값으로 현재까지 크기가 8임을 바로 알 수 있다.

i=4 일 때도 마찬가지로 바로 크기가 9임을 알 수 있다. 이 크기가 isPossible(int limit)에서 limit값을 초과하게 되면 불가능한 경우가 된다. (현재 W=0 이므로)
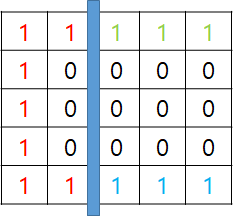
그럼 W가 1이라면 어떨까? limit이 8이라고 해보자. 그럼 위처럼 j=2, i=4 까지 봤을 때 크기가 9가 되어 limit을 넘어갔음을 알 수 있다. 그렇다면 j=1과 j=2 사이에 벽을 세우면 된다! 물론 남은 W가 없다면 (벽을 못 세운다면) 불가능한 경우이다. 벽을 세우면 아래 그림처럼 될 것이다. 끝까지 진행해보면 최대 크기는 7로, isPossible(8)은 limit 이내로 배치하는게 가능했으므로 true를 리턴할 것이다.
근데 여기서 문제가 생긴다. 이미 진행하면서 j=2, i=0일 때 분리집합에서 merge를 해버렸었다. 그리고 i=4일 때 limit을 넘어갔음을 알아챘으므로, 얘기한대로 벽을 치려면 merge한걸 취소해야 한다. 근데 분리 집합 알고리즘에서 merge를 취소하는 연산은 없다.
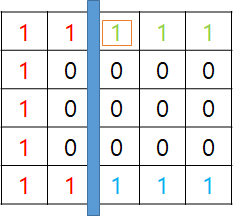
위에서 '셋 다 기본 아이디어는 동일하지만 구현 로직이 달랐다' 라고 말한 부분이 이 부분을 처리하는 로직이 모두 달랐다. 코드를 봤던 다른분의 코드의 경우, 한 분은 2차원 분리 집합 (2차원 dsu)으로 이 부분을 처리했고, 다른 분은 배열을 하나 더 두어서 처리했다. 내 경우엔 좀 무식한 방법으로 처리했는데, orders라는 리스트를 만들어서 분리 집합 알고리즘에서 사용한 parents 배열을 변경하는 모든 연산을 기록해뒀다. 그리고 벽을 세워야 할 경우, 해당 연산을 역순으로 되돌려서 merge를 취소했다. 즉, 미리 분리 집합 알고리즘을 적용하면 안되고 매번 isPossible()에서 분리집합을 새로 만들면서 연산을 기억하고 있다가 벽을 세워야하면 j-1 까지 진행한 연산을 취소해주는 식으로 진행한다. 분리집합 만드는건 현재 보고 있는 i, j 값 기준으로 i-1, j 가 1이면 merge하면 되고, i, j-1도 마찬가진데, 벽이 없는 경우에만 merge를 진행하면 된다.
...
int cur = -parents[find(ufIdx)];
if (cur > limit) {
if (wIdx == j) return false;
chk = false;
wIdx = j;
for (int k = orders.size()-1; k >= 0; k--) {
UfOrder curOrder = orders.get(k);
parents[curOrder.idx] = curOrder.bf;
}
orders = new ArrayList<>();
break;
}
...
결론적으로 '이 문제를 결정 문제로 보는 아이디어 + 일반적으로 존재하지 않는 분리 집합 알고리즘의 merge 취소 + 구현이 까다로움'이 합쳐진 상당히 어려운 문제였던 것 같다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<16);
public static void main(String[] args) throws Exception {
new Main().solution();
}
int r, c, w;
boolean[][] arr;
int[] parents;
List<UfOrder> orders = new ArrayList<>();
private void solution() throws Exception {
StringTokenizer st = new StringTokenizer(br.readLine());
r = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
w = Integer.parseInt(st.nextToken());
arr = new boolean[r][c];
for (int i = 0; i < r; i++) {
String row = br.readLine();
for (int j = 0; j < c; j++) {
arr[i][j] = row.charAt(j) == '1';
}
}
parents = new int[r*c];
int start = 0;
int end = 1000000;
while (start<=end) {
int mid = (start+end)/2;
Arrays.fill(parents, -1);
orders = new ArrayList<>();
if (!isPossible(mid))
start = mid+1;
else
end = mid-1;
}
System.out.println(start);
}
private int find(int a) {
if (parents[a] < 0) return a;
orders.add(new UfOrder(a, parents[a]));
return parents[a] = find(parents[a]);
}
private void union(int a, int b) {
a = find(a);
b = find(b);
if (a == b) return;
int hi = parents[a]<=parents[b]?a:b;
int lo = parents[a]<=parents[b]?b:a;
orders.add(new UfOrder(hi, parents[hi]));
parents[hi]+=parents[lo];
orders.add(new UfOrder(lo, parents[lo]));
parents[lo] = hi;
}
private boolean isPossible(final int limit) {
int j = 0;
int wIdx = 0;
for (int wCnt = 0; wCnt <= w && j < c; wCnt++) {
boolean chk = true;
while (j<c) {
for (int i = 0; i < r && j < c; i++) {
if (!arr[i][j]) continue;
int ufIdx = i*c+j;
if (i-1>=0 && arr[i-1][j]) {
int otherIdx = (i-1)*c+j;
union(ufIdx, otherIdx);
}
if (j-1>=0 && j-1>=wIdx && arr[i][j-1]) {
int otherIdx = i*c+(j-1);
union(ufIdx, otherIdx);
}
int cur = -parents[find(ufIdx)];
if (cur > limit) {
if (wIdx == j) return false;
chk = false;
wIdx = j;
for (int k = orders.size()-1; k >= 0; k--) {
UfOrder curOrder = orders.get(k);
parents[curOrder.idx] = curOrder.bf;
}
orders = new ArrayList<>();
break;
}
}
if (chk) {
j++;
// orders = new ArrayList<>();
}
else break;
}
}
return j == c;
}
}
class UfOrder {
int idx;
int bf;
public UfOrder(final int idx, final int bf) {
this.idx = idx;
this.bf = bf;
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 2632 - 피자판매 (java) (0) | 2023.07.20 |
|---|---|
| [자바] 백준 1263 - 시간 관리 (java) (0) | 2023.07.20 |
| [자바] 백준 2343 - 기타 레슨 (java) (0) | 2023.07.17 |
| [자바] 백준 14204 - 표 정렬 (java) (0) | 2023.07.13 |
| [자바] 백준 24395 - 명진이의 신년계획 (java) (0) | 2023.07.13 |





댓글