문제 : boj19939
우선 K개의 바구니에 N개의 공을 나눠 담을 수 있는지 여부부터 확인해보자. 이건 쉽게 1+2+...+k 가 n보다 큰지 확인하면 된다. 등차수열의 합 공식을 사용하면 합을 쉽게 구할 수 있다. 등차수열 합 공식은 다음과 같다(n이 수의 개수, a가 첫 항의 값, l이 n번째 항의 값)
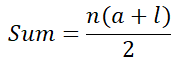
그리고 가장 많이 담긴 바구니와 가장 적게 담긴 바구니의 공의 차이가 최소가 되려면 어떻게 해야할지 생각해봐야 한다. 이 경우 직관적으로 k개를 1씩 차이를 내는게 최선임을 알 수 있다.
즉,
1. 1+2+...+K
2. 2+3+...+(K+1)
3. 3+4+...+(K+2)
...
과 같이 증가시키면서 N보다 커지는 순간을 찾으면 최소값을 어디서 구해봐야할지 알 수 있다. (합은 위의 등차수열 공식으로 구할 수 있다.)
근데 위에서 구한 값으로 N이 나누어 떨어지지 않는다면 어떻게 할까? 예를들어 K=4인 경우를 생각해보자.
이 때 N이 10이라면
1+2+3+4 = 10 이므로 K-1이 최소가 된다.
그럼 N이 11이라면 어떻게 할까?
2+3+4+5 = 14 이므로 11을 나타낼 수 없다. 1+2+3+4에서 해결을 해야 한다.
1+2+3+5와 같이 끝 수를 +1 시켜주면 된다. 그럼 최소와 최대의 차이는 K가 될 것이다.
이번엔 N=12 이다.
이번엔 1+2+4+5와 같이 처리하면 된다. 빈 공간이 생겼으니 3번째 값을 변경해줄 수 있게 된 것이다. 마찬가지로 차이는 K이다.
이번엔 N=13이라면 1+3+4+5를 해주면 된다. 역시 차이는 K이다. N=14라면 첫 항을 증가시켜서 2+3+4+5를 해주면 된다.
이 때 잘 생각해보면, 1+2+...+K와 2+3+...+(K+1)은 합의 차이가 K이다. 첫 항이 1 증가될때마다 합이 K씩 증가하게 된다. 그리고 K이하의 차이에 대해서는 위처럼 끝부터 2번째 항까지 하나씩 증가시키면서 모두 처리할 수 있다. 따라서 다음의 로직이 증명된 셈이다.
1. 1+2+...+K 보다 N이 작다면 -1을 출력한다.
2. 첫 항을 1씩 증가시켜나가면서 N보다 커지기 직전을 찾는다. N이 해당 등차수열 합으로 나누어떨어진다면 K-1이 답이고, 그렇지 않다면 K가 답이다.
PS. .. 해설을 쓰다보니 애초에 아래의 getArithmeticSequenceSum 함수처럼 매번 등차수열 합을 구하지 않고, 어차피 각 등차수열 합의 차이가 K이니 나누기 연산으로 한방에 구할 수 있을 것 같다ㅋㅋㅋ 하지만 이미 다 적었으니 패스!
PS2. 내 경우 수학이 많이 약하다보니 체감 난이도는 골드였다... ㅠ
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private int getArithmeticSequenceSum(int s, int e, int k) {
return (s+e)*k/2;
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int prevSum = getArithmeticSequenceSum(1,k,k);
if (n<prevSum) {
System.out.println(-1);
return;
}
int i = 2;
while (true) {
int curSum = getArithmeticSequenceSum(i,k+i-1, k);
if (curSum>n) {
if (prevSum == n)
System.out.println(k-1);
else
System.out.println(k);
return;
}
prevSum = curSum;
i++;
}
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 2480 - 주사위 세개 (boj java) (0) | 2022.05.09 |
|---|---|
| [자바] 백준 12981 - 공 포장하기 (boj java) (0) | 2022.05.08 |
| [자바] 백준 22155 - Простая задача (boj java) (0) | 2022.05.06 |
| [자바] 백준 24586 - Code Guessing (boj java) (0) | 2022.05.05 |
| [자바] 백준 1388 - 바닥 장식 (boj java) (0) | 2022.05.04 |





댓글