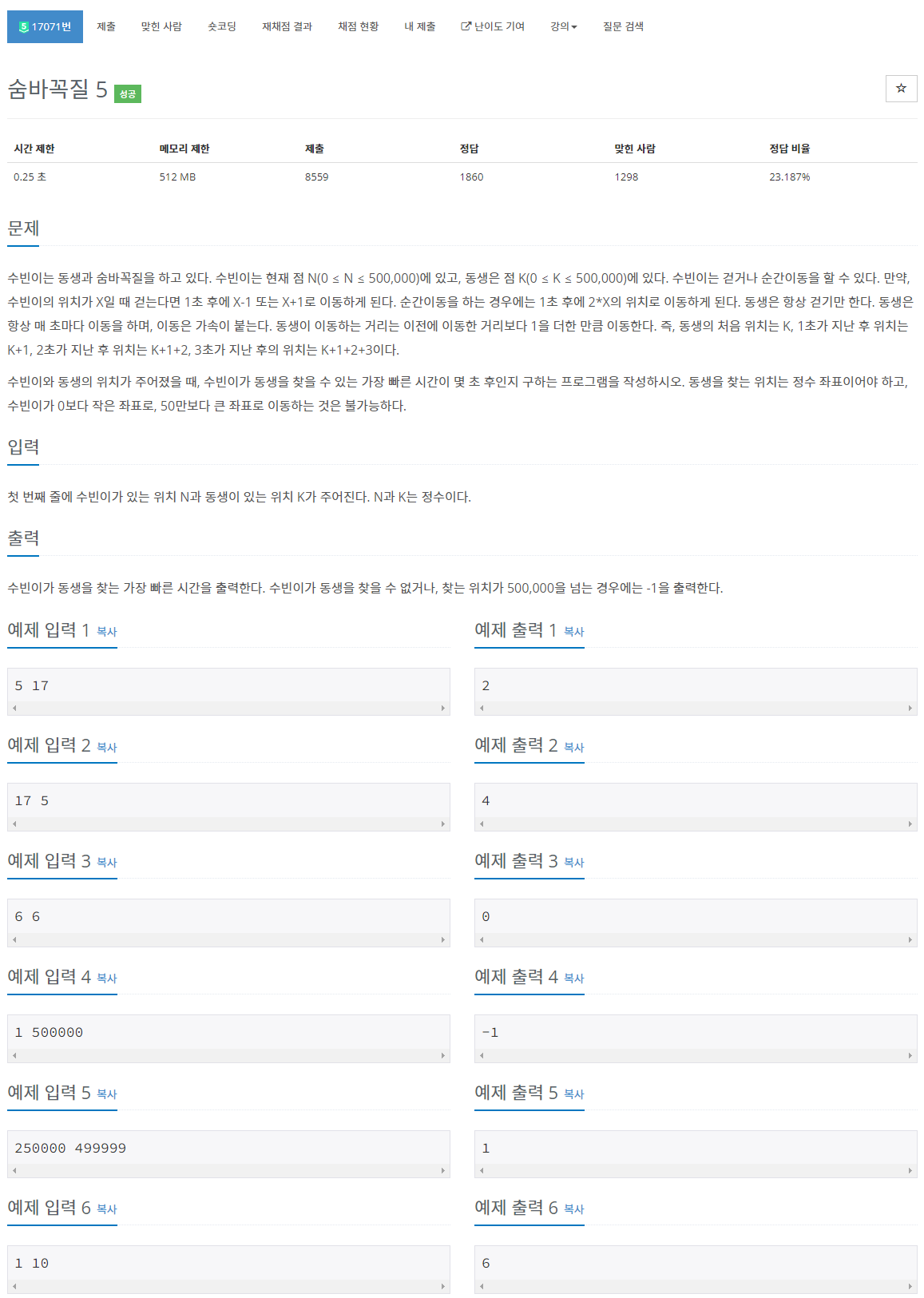
문제 : boj17071
필요 알고리즘 개념
- 그래프, BFS (너비 우선 탐색)
- 결론적으로 보면 그냥 BFS 문제이다. 다만 아이디어가 좀 필요하다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
생각 과정 및 풀이
이 문제의 경우 상당히 많이 잘못 생각했고, 결론적으로 proof by AC (정답 맞췄으니 증명됬다!) 느낌으로 풀었다 ㅋㅋ. 그러니 풀이를 생각한 과정을 적어보겠다. 정답 코드만 볼꺼면 맨 아래의 코드만 보면 될 것 같다.
우선 내 기본 아이디어는, 어차피 동생의 위치는 시간별로 고정되어 있으므로 전처리로 미리 구해두면 된다는 점이었다. 50만 이하까지 시간대별로 동생이 있는 위치를 미리 구해두므로, POSITION의 size가 곧 50만을 넘지 않는 최대 시간이 된다. 또한 BFS로 수빈이의 위치를 바꿀 때, 처음 위치부터 걸린 시간을 체크하면 해당 시간에서의 동생의 위치를 O(1)로 알 수 있다. 이건 오답과정부터 풀이때까지 변경되지 않는 기본 아이디어였으므로 미리 설명한다.
class SiblingPosition {
ArrayList<Integer> POSITION = new ArrayList<>();
public SiblingPosition(int k) { // 동생의 처음 위치 k를 받아 전처리
int weight = 0;
while ((k += weight++)<=Config.LIMIT.getValue()) // LIMIT은 50만이다.
POSITION.add(k);
}
int getMovedLocation(int dist) {
return POSITION.get(dist);
}
int size() {
return POSITION.size();
}
}
오답 1. 방문체크가 애매해서 일단 제출해봤다.
예제 입력 2를 보자. 동생이 5->6->8->11->15 로 움직이는 동안, 수빈이는 17->16->15->14->15 처럼 움직여야 예제 출력 2처럼 4의 시간에 만날 수 있다. 즉, 방문체크를 일반적인 BFS 방식처럼 한 번 도착했다고 다시 방문하지 못하게 하면 안된다는 점은 파악할 수 있었다. 하지만 어떻게 방문체크해야할지 떠오르지 않아서 우선 방문체크 없이 제출해봤고, 당연히 메모리 초과였다.
Queue<Position> q = new ArrayDeque<>();
q.add(new Position(N, 0));
while (!q.isEmpty()) {
Position cur = q.poll();
if (cur.checkMeet(siblingPosition)) {
System.out.println(cur.dist);
return;
}
for (Move movement : MOVEMENTS) {
int nextN = movement.nextPosition(cur.n);
Position next = new Position(nextN, cur.dist+1);
if (!next.isValidPosition() || next.dist >= siblingPosition.size())
continue;
q.add(next);
}
}
오답 2. true, false 방문체크대신 현재까지 해당 위치에 도달한 최소 시간으로 방문체크를 해봤다.
단순한 true, false 방문체크로는 답이 안나올 것 같아서 방문체크(v[])에 현재까지 해당 위치에 도달한 가장 짧은 시간을 써두고, 그것과 동일하거나 오래걸려서 도달한 경우를 제외하기로 했다. 그렇다고 해도 17->16->15->14->15 와 같은 경우 앞의 15보다 뒤의 15가 늦게 도착한 것이니 방문체크에는 '2'만 써있을 것이다. 하지만 실제론 '4'에서도 도달했다. 이걸 답으로 확인하기 위해, 좌우로 왔다갔다 해서 제자리로 돌아온 경우 +2씩 시간이 추가될 것이므로 동생의 시간대별 위치와 짝수만큼의 차이가 난다면 그건 도달한 것으로 생각하는 로직을 추가했다. 이건 "틀렸습니다." 가 떴다. 어쨌든 개인적으로 메모리초과보다는 그냥 틀렸습니다 뜨는게 더 파악하기 쉬우므로 다행이었다(?). 하지만 더이상 방법이 생각 안났다.
Queue<Position> q = new ArrayDeque<>();
int[] v = new int[Config.LIMIT.getValue()+1];
Arrays.fill(v, Integer.MAX_VALUE);
q.add(new Position(N, 0));
v[N] = 0;
while (!q.isEmpty()) {
Position cur = q.poll();
if (cur.checkMeet(siblingPosition)) { // BFS 진행 중 만났다면 거기서 끝내면 됨.
System.out.println(cur.dist);
return;
}
for (Move movement : MOVEMENTS) {
int nextN = movement.nextPosition(cur.n);
Position next = new Position(nextN, cur.dist+1);
if (!next.isValidPosition() || v[nextN]<=next.dist || next.dist >= siblingPosition.size())
continue; // v[] 에 현재까지 해당 위치에 도달한 최소 시간이 써있다.
v[nextN] = next.dist; // 아직 해당 위치에 도착하지 못했거나, 기존 v[]에 써있던 것보다 빨리 도착 한 경우만 체크한다.
q.add(next);
}
}
// BFS 진행중엔 만나지 못했지만, 15->14->15->14->15 처럼 한 자리에서 왔다갔다 하면서 제자리에
// 머물 경우를 체크해주기 위한 로직이다.
int min = Integer.MAX_VALUE;
for (int i = 0; i < siblingPosition.size(); i++) {
int cur = siblingPosition.getMovedLocation(i);
if (v[cur] > i) continue;
int gap = i - v[cur];
if (gap%2==0 && min>i) {
min = i;
}
}
System.out.println(min == Integer.MAX_VALUE ? -1 : min);
풀이
'오답2'에서 더이상 어제는 생각이 안났다. 이럼 보통 자고 일어나면 아이디어가 생길 경우가 많아서 일단 잤고, 아침에 해결할 수 있었다ㅋㅋ. 풀이 아이디어가 떠오른건 아니고, 반례를 생각해본 것이다. 난 5->4->5->4->5 이런식으로 좌우로 왔다갔다 하는 부분만 생각했는데, 잘 생각해보니 이런 경우도 있다 "5->4->3->2->4->5". 즉, x2 가 가능해서 무조건 차이가 2로 나누어 떨어지는 것만 체크하면 안됬던 것이다. 홀수로 차이가 나도 가능한 경우가 있을 수 있는 것이다.
이걸 해결하기 위해 방문체크를 홀수와 짝수 두 종류로 나누었다. v[a][b] 에서 a는 0~500,000 으로 위치를 나타내고, b는 0이면 짝수 1이면 홀수를 나타낸다. 즉 v[a][b]는 a의 위치에 시간이 짝수(b=0) 또는 홀수(b=1)일 때 도착한 최소 시간 으로 정의된다. 그럼 아래와 같이 구현할 수 있고, 정답이었다. proof by AC 라고 말 한 이유는 수학적으로 증명은 못하겠기 때문이다. 사실상 오답 과정 및 반례를 해결하는 과정에서 얻어걸린 풀이이다.
q.add(new Position(N, 0));
v[N][0] = 0;
int min = Integer.MAX_VALUE;
while (!q.isEmpty()) {
Position cur = q.poll();
// 어차피 모든 경우를 본 후 체크해도 똑같아서 그냥 BFS 중엔 체크를 안하기로 했다.
for (Move movement : MOVEMENTS) {
int nextN = movement.nextPosition(cur.n);
Position next = new Position(nextN, cur.dist+1);
if (!next.isValidPosition() || v[nextN][next.dist%2]<=next.dist || next.dist >= siblingPosition.size())
continue;
v[nextN][next.dist%2] = next.dist; // 이제 홀짝을 나눠서 생각한다.
q.add(next);
}
}
for (int i = 0; i < siblingPosition.size(); i++) { // 동생이 50만 이하에서 존재할 수 있는 모든 시간당 위치에 대해
int cur = siblingPosition.getMovedLocation(i); // cur은 i시간에서 동생의 위치
if (v[cur][i%2] > i) continue; // 동생의 위치의 홀짝 여부에 따라 최소로 도착한 시간(v[a][b])이 동생보다 뒤에 도착한거면 무시한다.
if (min>i) { // 그렇지 않다면 동생과 만날 수 있는 경우이므로, 최소 시간을 min에 넣어준다.
min = i;
}
}
System.out.println(min == Integer.MAX_VALUE ? -1 : min); // min이 초기값과 동일하다면 동생과 못만난것이니 -1을 출력해주고, 아니라면 min을 출력해준다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
interface Move {
int nextPosition(int cur);
}
class PlusMove implements Move {
@Override
public int nextPosition(int cur) {
return cur+1;
}
}
class MinusMove implements Move {
@Override
public int nextPosition(int cur) {
return cur-1;
}
}
class MultipleMove implements Move {
@Override
public int nextPosition(int cur) {
return cur*2;
}
}
enum Config {
LIMIT(500000);
private int config;
private Config(int config) {
this.config = config;
}
int getValue() {
return this.config;
}
}
class SiblingPosition {
ArrayList<Integer> POSITION = new ArrayList<>();
public SiblingPosition(int k) {
int weight = 0;
while ((k += weight++)<=Config.LIMIT.getValue())
POSITION.add(k);
}
int getMovedLocation(int dist) {
return POSITION.get(dist);
}
int size() {
return POSITION.size();
}
}
class Position {
int n, dist;
public Position(int n, int dist) {
this.n = n;
this.dist = dist;
}
public boolean isValidPosition() {
return this.n>=0 && this.n<=Config.LIMIT.getValue();
}
public boolean checkMeet(SiblingPosition siblingPosition) {
return this.n == siblingPosition.getMovedLocation(this.dist);
}
}
public class Main {
private final Move[] MOVEMENTS = {new MinusMove(), new PlusMove(), new MultipleMove()};
private SiblingPosition siblingPosition;
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
siblingPosition = new SiblingPosition(K);
Queue<Position> q = new ArrayDeque<>();
int[][] v = new int[Config.LIMIT.getValue()+1][2];
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[0].length; j++)
v[i][j] = Integer.MAX_VALUE;
}
q.add(new Position(N, 0));
v[N][0] = 0;
int min = Integer.MAX_VALUE;
while (!q.isEmpty()) {
Position cur = q.poll();
for (Move movement : MOVEMENTS) {
int nextN = movement.nextPosition(cur.n);
Position next = new Position(nextN, cur.dist+1);
if (!next.isValidPosition() || v[nextN][next.dist%2]<=next.dist || next.dist >= siblingPosition.size())
continue;
v[nextN][next.dist%2] = next.dist;
q.add(next);
}
}
for (int i = 0; i < siblingPosition.size(); i++) {
int cur = siblingPosition.getMovedLocation(i);
if (v[cur][i%2] > i) continue;
if (min>i) {
min = i;
}
}
System.out.println(min == Integer.MAX_VALUE ? -1 : min);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 20976 - The Second Largest Integer (java) (0) | 2022.12.02 |
|---|---|
| [자바] 백준 8949 - 대충 더해 (java) (0) | 2022.11.30 |
| 백준 2563 - 색종이 (자바, C, C++, node.js, Kotlin, Python, C#) (1) | 2022.11.29 |
| [자바] 백준 23972 - 악마의 제안 (java) (0) | 2022.11.28 |
| [자바] 백준 6763 - Speed fines are not fine! (java) (0) | 2022.11.27 |





댓글