문제 : boj1671
문제에서 제시된 상황이 그래프로 표현 가능한 경우 그래프로 바꿔서 생각해보는 것이 이득인 경우가 많다. 이 문제의 경우에도 주어진건 상어의 크기, 속도, 지능으로 3개나 되지만, 사실 그래프의 간선으로 생각해본다면 값이야 어떻든 조건을 만족한 경우 그냥 방향이 있는 간선 하나가 추가될 뿐이다. 예시 입력 1을 그려보면 다음과 같다. 간선은 [먹는쪽 -> 먹히는쪽]으로 연결할 것이다.
5
4 5 5
10 10 8
5 7 10
8 7 7
8 10 3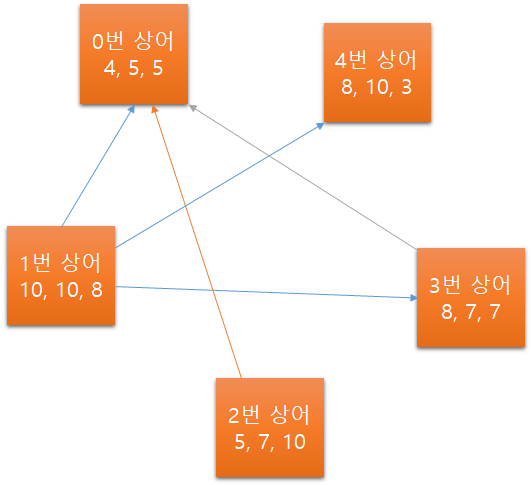
그럼 동일 정점을 좌우로 둬서 다음과 같이도 그려볼 수 있다.
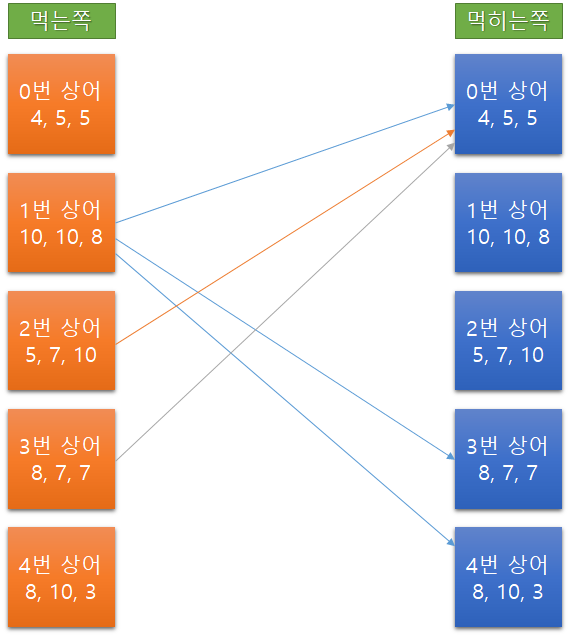
결국 최대한 많이 잡아먹으면 남아 있는 수가 최소가 되므로, 최대유량 문제인데 이분그래프 이므로 이분매칭을 사용해서 좌측의 상어가 우측의 상어를 먹는다고 생각해보자. 그리고 좌측에서 우측으로 2개를 매칭 시킬 수 있다고 해보면 이분매칭으로 이 문제를 풀 수 있다. 이분매칭에 대한 설명은 따로 적어둔게 없어서 여기(유투브 - MIT OpenCourseWare - Bipartite Matching) 등을 참고하자. 결론적으로 이분매칭을 진행하면서, 매칭이 가능한 경우의 수를 세고 그걸 cnt라고 할 때 N-cnt가 답이 될 것이다.
문제에서 먹는 순서에 따라 뭔가 최소수치가 다를 것 같이 설명을 해둬서 어떻게 처리할지 궁금할 것이다. 하지만 먹는 순서야 어떻든, 누가 누굴 먹을지만 정해지면 어떻게든 최소 수치가 되도록 먹는 순서는 조정할 수 있다. 따라서 먹는순서는 전혀 상관이 없다. 필요한건 누가 누굴 먹을 수 있는지와 최대 2명씩 먹어서 최대한 많이 매칭을 시키는 것이다.
이 때 주의가 필요한 경우는 두 상어의 크기, 속도, 지능이 셋 다 동일할 경우이다. 이 경우 서로가 서로를 먹을 수 있으므로 별도로 처리를 해주지 않으면 틀리게된다. 다행히 문제에서 이 부분을 생각할 수 있도록 예제 입력 4에서 예시로 들어줬다.
이 경우 단순히 N-cnt가 0이라고 해서(모두 서로가 서로를 먹어서 없어진 경우) 한마리는 남아야 하니 1이라고 출력하게 되면 틀리게된다. 왜냐하면 다음과 같은 케이스를 처리할 수 없기 때문이다.
3
1 5 9
1 5 9
9 5 1위의 경우 9 5 1인 상어와 1 5 9인 상어는 서로 먹지 못한다. 1 5 9는 서로 먹을 수 있는데, 한마리는 당연히 남아야 한다. 따라서 답은 2가 되야 하고, 단순히 N-cnt가 0이라고 1로 출력하는건 이 케이스를 처리할 수 없다. 그렇다고 크기, 속도, 지능이 동일한 상어중에 무조건 하나를 남겨서도 안된다. 다음의 케이스를 보자. 위의 케이스를 약간 변경한 아래의 케이스는 답이 1이 되어야 하기 때문이다.
3
1 5 9
1 5 9
1 6 10
이건 약간의 스위핑 개념을 넣으면 되는데, 크기, 속도, 지능이 동일한 경우에만 먹는 방향을 하나로 고정하는 것이다. 즉 입력으로 들어온 순서를 기준으로 인덱스가 큰게 작은걸 먹든, 작은게 큰걸 먹든 아무튼 방향을 고정하면 된다. 이 부분을 처리하는게 코드의 53line이다. 이렇게하면 크기, 속도, 지능이 동일한 케이스를 문제없이 처리할 수 있다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
class Shark {
int a,b,c;
public Shark(int a, int b, int c) {
this.a = a;
this.b = b;
this.c = c;
}
public boolean canEat(Shark ano) {
if (this.a>=ano.a && this.b>=ano.b && this.c>=ano.c)
return true;
return false;
}
}
int[] matched;
boolean[] v;
ArrayList<Integer>[] edges;
int n;
private boolean matching(int from) {
for (int i = 0; i < edges[from].size(); i++) {
int to = edges[from].get(i);
if (v[to]) continue;
v[to] = true;
if (matched[to] == -1 || matching(matched[to])) {
matched[to] = from;
return true;
}
}
return false;
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
edges = new ArrayList[n];
matched = new int[n];
Arrays.fill(matched, -1);
for (int i = 0; i < n; i++) edges[i] = new ArrayList<>();
Shark[] arr = new Shark[n];
StringTokenizer st;
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
arr[i] = new Shark(a,b,c);
for (int j = 0; j < i; j++) {
if (arr[i].canEat(arr[j]) && arr[j].canEat(arr[i])) edges[i].add(j);
else if (arr[i].canEat(arr[j])) edges[i].add(j);
else if (arr[j].canEat(arr[i])) edges[j].add(i);
}
}
int cnt = 0;
for (int j = 0; j < 2; j++) {
for (int i = 0; i < n; i++) {
v = new boolean[n];
if (matching(i)) {
cnt++;
}
}
}
System.out.println(n-cnt);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 24480 - 알고리즘 수업 - 깊이 우선 탐색 2 (boj java) (0) | 2022.05.28 |
|---|---|
| [자바] 백준 2559 - 수열 (boj java) (0) | 2022.05.27 |
| [자바] 백준 11660 - 구간 합 구하기 5 (boj java) (0) | 2022.05.26 |
| [자바] 백준 21939 - 문제 추천 시스템 Version 1 (boj java) (0) | 2022.05.25 |
| [자바] 백준 18221 - 교수님 저는 취업할래요 (boj java) (0) | 2022.05.24 |





댓글