문제 : boj5419
1. 일단 모든 쌍을 직접 확인해보자! (brute force)
n개의 정점 모두에 대해 모든 쌍을 확인하면서 조건을 만족하는지 확인해보면 된다. 이 경우 코드는 아래와 같이 될 것이다. 물론 이대론 O(N^2)이 되므로 시간 내에 통과할 수 없다! 어쨌든 어떠한 점이 자신보다 x가 작거나 같고, y가 크거나 같은지 확인하면 될 것임을 알 수 있다.
ArrayList<Island> arr = new ArrayList<>();
void add(Island island) {
arr.add(island);
}
long getAnswer() {
long cnt = 0;
for (int i = 0; i < arr.size(); i++) {
for (int j = i+1; j < arr.size(); j++) {
Island a = arr.get(i);
Island b = arr.get(j);
if (a.x<=b.x && a.y>=b.y) cnt++;
else if (a.x>=b.x && a.y<=b.y) cnt++;
}
}
return cnt;
}
2. 규칙을 찾아보자!
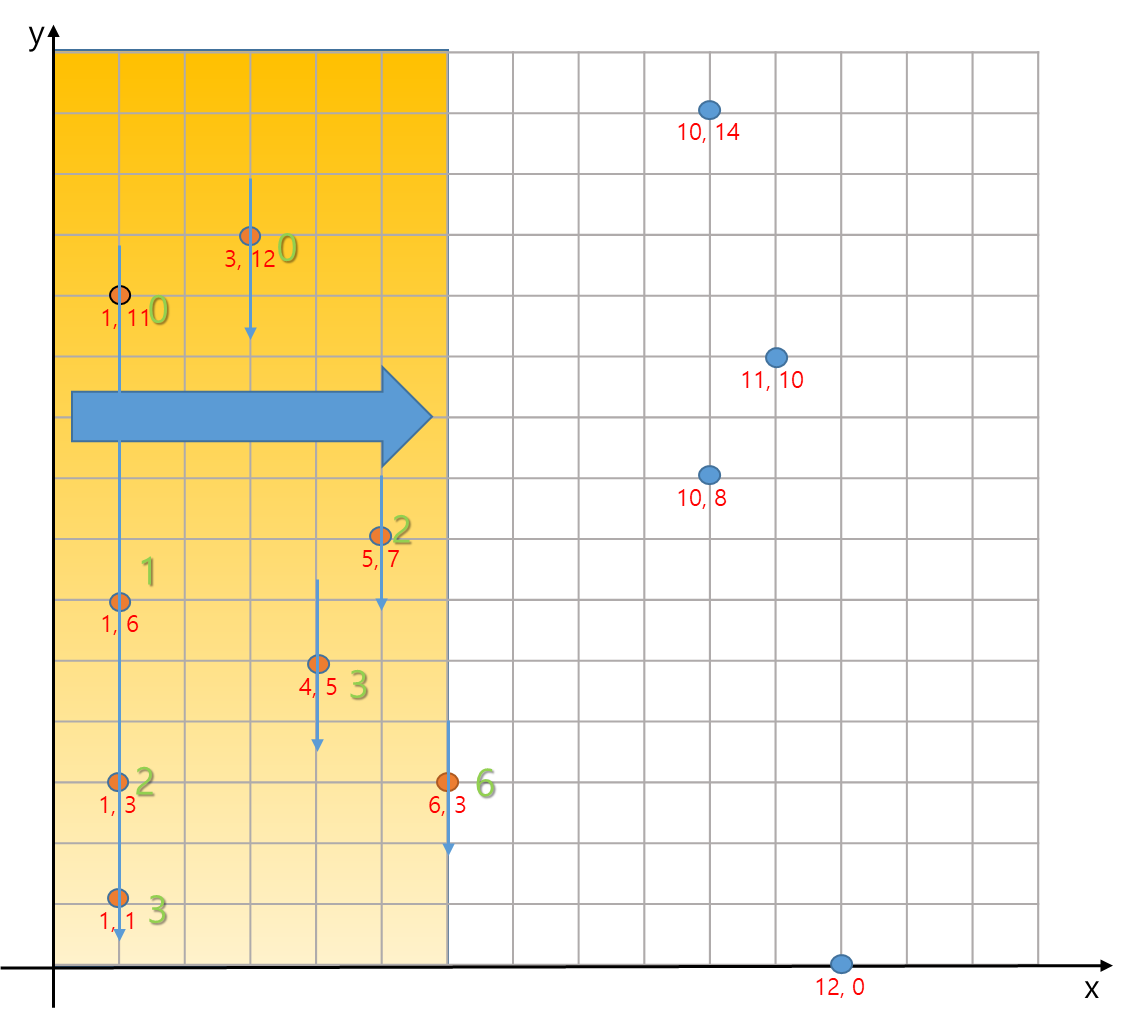
brute force로 모든 정점의 쌍을 확인하는건 효율적이지 않으므로 무리가 있다. 그럼 규칙을 한번 찾아보기 위해 일단 그려보자. 몇 개의 섬이 있는 테스트 케이스에서 대해 그림으로 그려보면 다음과 같다. 이하 그림에서 x=11, y=10인 지점에서 봤을 때 자기자신으로 올 수 있는 정점은 노란 부분에 포함된 3개가 된다.
즉, 2차원 좌표평면에 나타냈을 때 어떤 정점에서 자신의 2사분면에 해당하는 부분에 몇개의 정점이 있는지 파악하면 각 정점에서 몇 개가 되는지 파악해볼 수 있다.

3. 그래서 그걸 어떻게 구함?
각 정점들을 ORDER BY x ASC, y DESC 형태로 정렬해보자. 즉 x가 동일하다면 y 내림차순으로, x가 다르다면 x 오름차순으로 정렬하는것이다. f(a)를 a이상의 높이를 가진 정점의 개수라고 한번 정의해보자. 그리고 정렬된 순서대로 방문하면서 해당 정점의 y 높이를 기준으로 f(y)를 구하고, 마찬가지로 y값을 기준으로 해당 위치에 자신이 있었다고 체크하자. 즉, (1,11)을 방문했다면 f(11)을 구한 후, 높이 11의 카운팅을 +1 해주는 셈이다.
x가 증가하는 방향으로 진행하면서, 스캔하듯이 y축 기준으로 위에서 아래로 진행하면서 카운팅하면서 답을 구해내는 셈이다. 그렇게 하면 '2'와 같이 매번 자신의 2사분면에 해당하는 정점들의 개수를 알 수 있다.
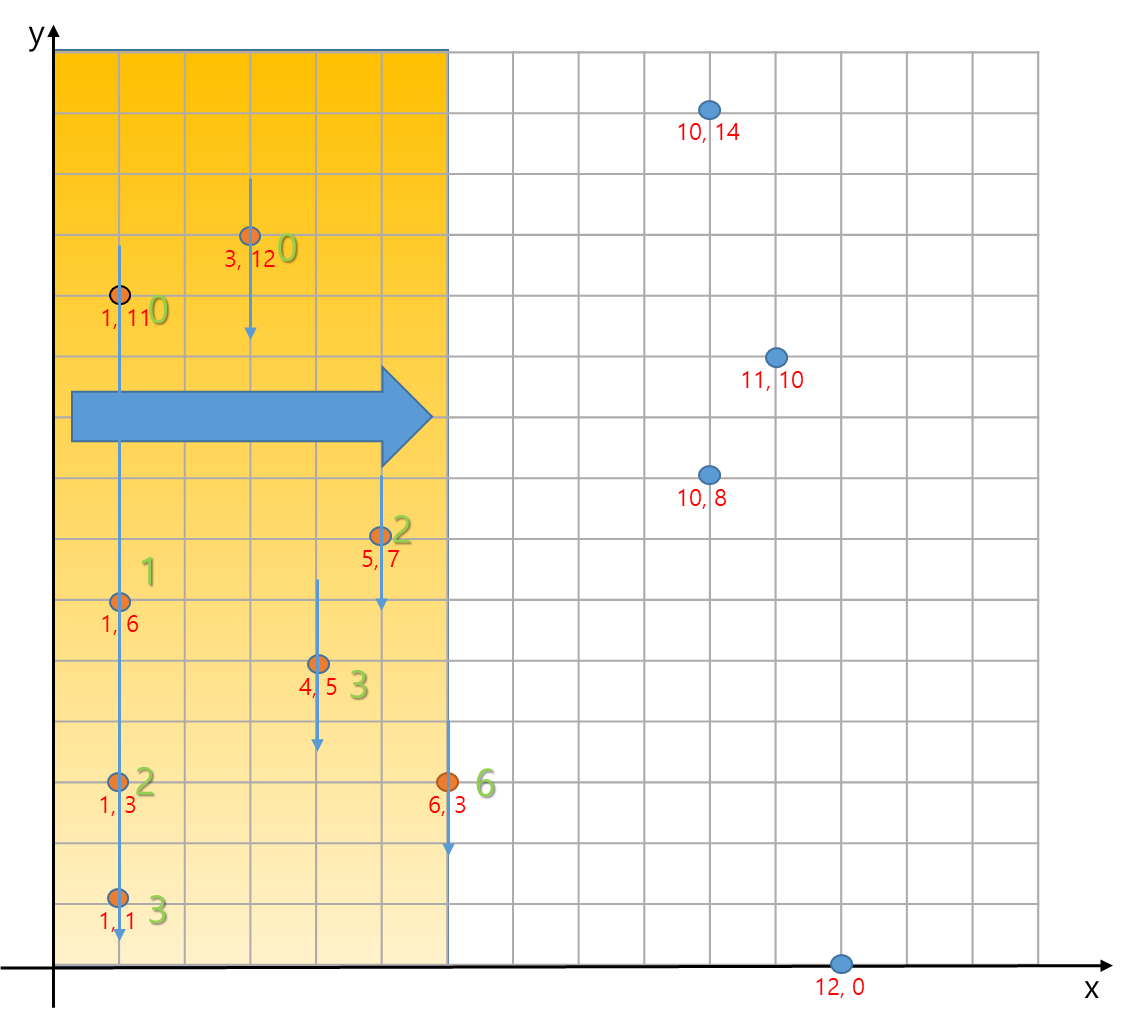
그렇게 구해보면 (6,3) 까지 진행하면 다음과 같이 구해진다. 녹색으로 써둔 것이 f(a) 값이다. 예를들어 (5,7) 지점은 f(7) 즉, 자신보다 x가 작으면서 y값이 7이상이었던 지점들의 수가 된다. 좌측부터 x값을 진행하면서 스캔하듯이 y 방향으로 위에서 아래로 훑으면서 지나오는 것이다(단, 정점이 존재하는 부분만)
4. 그래서 그게 brute force 보다 빠른가?
brute force는 항상 O(N^2) 이지만, '2'~'3'과 같이 진행할 경우 (1,5), (2,4), (3,3), (4,2), (5,1) 와 같은 형태의 최악의 경우에만 O(N^2)이 되고 그 외의 경우엔 brute force보다는 효율적으로 구할 수 있다. 하지만 어쨌든 최악의 경우엔 brute force와 동일하므로 역시 시간내에 통과할 수 없다.
그럼 이제 f(a)를 더 빠르게 구할 방법을 찾아야 한다! 결국 f(a)는 높이가 a 이상인 정점의 개수에 해당한다. 즉, 높이가 a 이상 최대치 이하인 '구간'의 어떠한 합계에 해당한다. 이걸 빠르게 구할 수 있는 자료구조 혹은 알고리즘을 찾으면 된다. 이 때 유용한 것이 세그먼트 트리와 제곱근 분할법이 있다. 그럼 각각 O(NlogN)과 O(Nsqrt(N))으로 시간복잡도를 줄일 수 있고, N이 최대 75000이므로 둘 다 통과하는데 문제 없다.
5. 근데 20억개 구간에 대해 세그먼트 트리나 제곱근 분할법 적용이 가능함?
사실 세그먼트 트리 또는 제곱근 분할법이 생각났다 하더라도 문제인게, 둘 중 어떤걸 쓰더라도 높이가 -10^9~10^9 이므로 총 20억개의 구간에 대해 유지한다면 당연히 메모리 초과와 시간 초과가 나게 된다.
근데 N이 최대 75000이므로, 구간의 범위야 어떻게 되든 서로 다른 높이의 수치는 최악의 경우라도 75000가지만 존재한다. 따라서 이걸 0~74999의 값으로 압축시킬 수 있다. 예를들어 n=5이고 y값만 봤을 때 -1000000000, 10, -5, 30, 1000000000 이라고 해보자. 이 값들을 정렬한 후 값을 압축하면 다음과 같이 바꿔쓸 수 있다.
-1000000000 -> 0
-5 -> 1
10 -> 2
30 -> 3
1000000000 -> 4
그럼 좌측을 key, 우측의 압축된 결과를 value로 하는 HashMap을 유지한다면 입력값과 관계없이 0 이상 75000 미만의 구간을 가진 구간이 된다.
6. 결론은 구현이 빡쌘 문제이다.
애초에 아이디어 자체는 공책에 한 번 그려보면 그리 어렵지 않게 떠올릴 수 있다. 다만 특정 구간의 합 같은걸 더 빠르게 구할 수 있는 알고리즘을 모른다면, brute force로 모든 쌍을 보는 것과 차이점을 찾기 힘들기 때문에 풀이를 파악하기 힘들 것이다. 아무튼 아이디어가 떠올랐더라도 구현이 빡쌘 문제임에는 틀림없다.
아무튼 내 경우엔 제곱근 분할법을 사용했다. 세그먼트 트리가 더 효율적이긴 하지만, 제곱근 분할법이 좀 더 직관적으로 이해하기가 편하고 구현하기도 편해서(상대적으로) 제곱근 분할법을 더 애용한다. 보통 빡빡하게 복잡도가 설정된 문제가 아니라면 제곱근 분할법으로도 충분하다. 모른다면 여기를 참고하자.
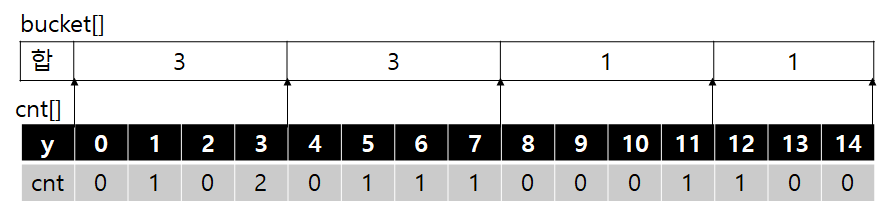
대강 설명하면, 높이의 구간 수에 대해 cnt라는 배열로 카운팅을 한다. 예를들어 현재 봤던 정점이 (3,12)라면 cnt[12]의 값을 +1 시켜주는 식이다. 그리고 cnt 배열을 sqrt(높이의 구간 수) 만큼 나눠서 별도로 카운팅한다. 이걸 bucket이라 부르겠다. '3'에서 예시로 나타냈던 다음 그림을 보자.
(6,3) 까지 진행한 결과에 대해 cnt와 bucket은 다음과 같이 될 것이다. 높이 구간은 총 0~14까지이므로 sqrt(15)를 내림하면 4가 된다. 즉 총 14개의 카운팅 값을 4개씩 묶어서 별도로 카운팅 합을 유지하는 것이다. 유지하는건 간단하다! 아까 구해둔 sqrt(15) 값을 사용해서, y=12를 카운팅 한다면 cnt[12] += 1; 후에 bucket[12/4] += 1; 를 해주면 된다.
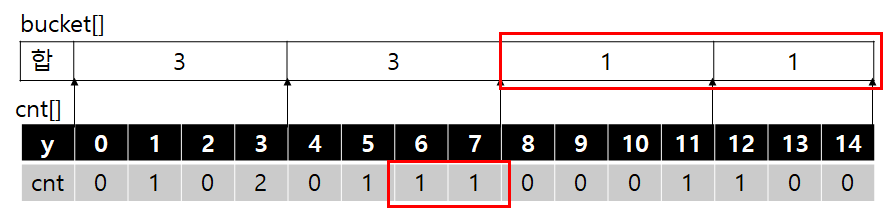
그럼 f(6). 즉, 6 이상의 높이를 가진 정점의 개수는 아래와 같은 부분들을 합해서 구할 수 있다.
f(0)은 다음과 같다.
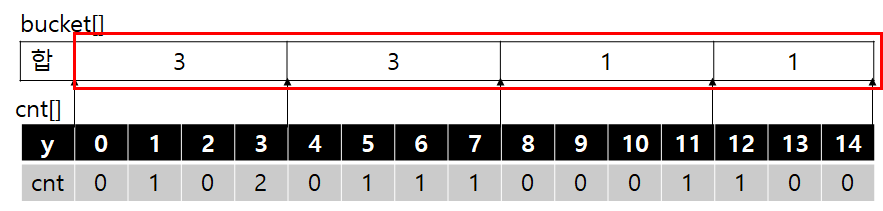
위와 같이 bucket에 온전히 포함된 구간은 바로 더하고, 구간에 부분적으로 걸친 구간은 직접 cnt에서 한땀한땀 더해주는 것이다. 이 경우 bucket은 최대 sqrt(N)개가 존재하고, 부분적으로 걸친 구간 또한 최대 sqrt(N)개만 존재하므로 매번 O(sqrt(N) + sqrt(N)) = O(sqrt(N))이 되는 것이다.
코드에서 pq는 정점들을 정렬하기 위해 사용한 것이고, yChk와 yPq, comp는 좌표(값) 압축을 위해 사용했다. 이외에 bucket, cnt는 위에 설명한 것과 동일한 명칭을 사용했다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
class Island implements Comparable<Island> {
int x, y;
public Island(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Island o) {
if (this.x == o.x)
return o.y - this.y;
return this.x - o.x;
}
}
public class Main {
PriorityQueue<Island> pq;
HashSet<Integer> yChk;
PriorityQueue<Integer> yPq;
HashMap<Integer, Integer> comp;
int compSize, sqrtN;
int[] bucket, cnt;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private void init() {
pq = new PriorityQueue<>();
yChk = new HashSet<>();
yPq = new PriorityQueue<>();
comp = new HashMap<>();
}
private void initIsland() throws Exception {
int n = Integer.parseInt(br.readLine());
while (n-->0) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
pq.add(new Island(x, y));
if (!yChk.contains(y)) {
yChk.add(y);
yPq.add(y);
}
}
}
private void compressionY() {
int compNum = 0;
while (!yPq.isEmpty()) {
comp.put(yPq.poll(), compNum++);
}
compSize = compNum;
}
private long getOverCnt(int y) {
long totalCnt = 0;
while (y%sqrtN != 0 && y!=compSize)
totalCnt += cnt[y++];
if (y != compSize) {
for (int i = y / sqrtN; i < bucket.length; i++) {
totalCnt += bucket[i];
}
}
return totalCnt;
}
private void add(int y) {
cnt[y]++;
bucket[y/sqrtN]++;
}
private long getAnswer() {
sqrtN = (int)Math.sqrt(compSize);
if (sqrtN == 0) sqrtN = 1;
bucket = new int[compSize/sqrtN+1];
cnt = new int[compSize];
long sum = 0;
while (!pq.isEmpty()) {
Island cur = pq.poll();
sum += getOverCnt(comp.get(cur.y));
add(comp.get(cur.y));
}
return sum;
}
private void solution() throws Exception {
int tc = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while (tc-->0) {
init();
initIsland();
compressionY();
sb.append(getAnswer()).append('\n');
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 3029 자바 - 경고 (boj 3029 java) (0) | 2022.04.02 |
|---|---|
| 백준 1187 자바, C++ - 숫자 놀이 (boj 1187 java c++) (0) | 2022.04.01 |
| 백준 1918 자바 - 후위 표기식 (boj 1918 java) (2) | 2022.03.31 |
| 백준 2170 자바 - 선 긋기 (boj 2170 java) (0) | 2022.03.30 |
| 백준 16496 자바 - 큰 수 만들기 (boj 16496 java) (0) | 2022.03.30 |





댓글